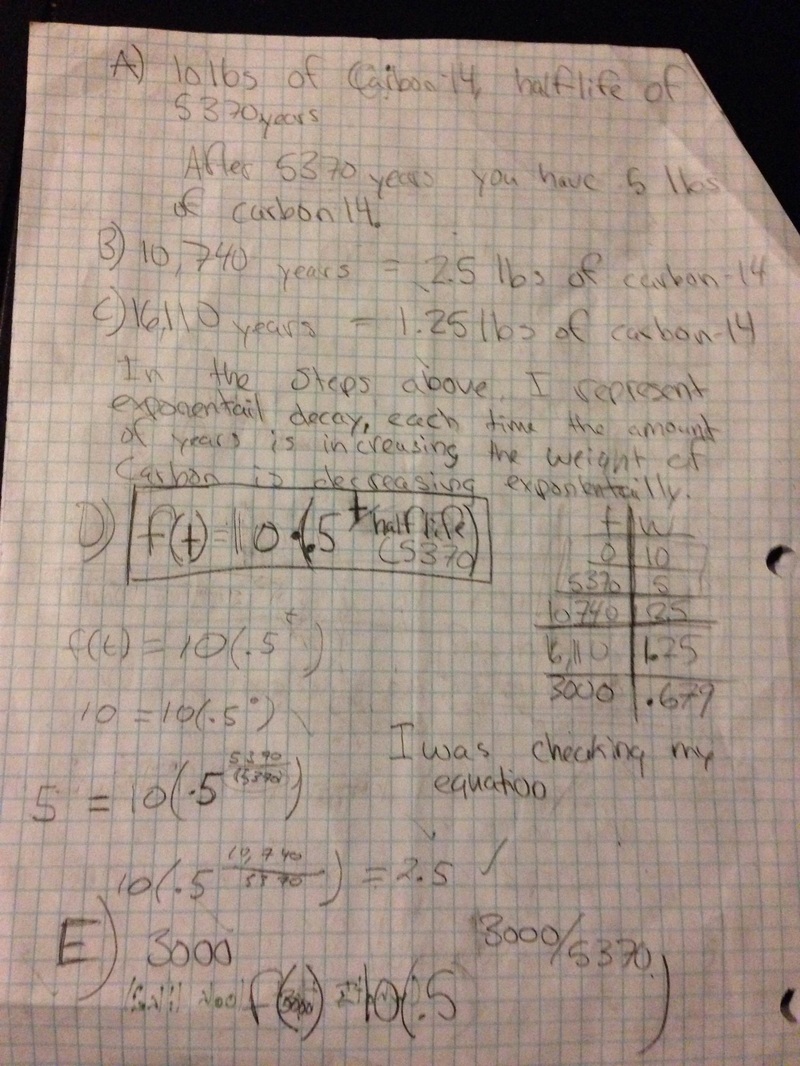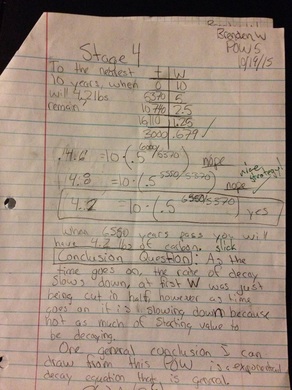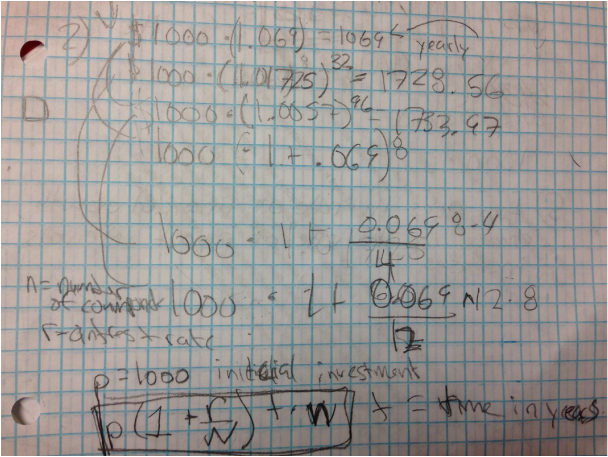Algebra 2 Final DP Update
Generating Ideas
For the final project Tj and I had created an exploration that walked people through simple step conversion problems. This exploration exemplified one habit of a mathematician that I did very well but instead of generating multiple ways of approaching a problem, we thought about problems that proved different conversions but that were all still simple. This included having to convert different ways, for example we have a couple of problems using currency, some about weight, and also some about volume. One way we could have expressed this habit more is if we created a problem that helped the audience set up the measurements over each other so they could see how they cross cancel.
Communicating Thinking in a Clear and Accessible Way
Through the second semester I felt like I was much more comfortable conveying my ideas and approach to problems, even if I wasn't sure on the answer. Explorations often throw new content at me and therefor I approach each problem from a problem-solving perspective instead of a math problem. This sometimes leads to me doing problems in a very unconventional way, and when we review the homework the next day, I have had to learn how to walk people through my crazy steps and thinking. Although I am usually able to find some kind of approach to a problem, sometimes I am not able to and need to listen to the ways my peers went. Unfortunately, when I do not understand I often lose sight of actually learning the problem, and instead focus on just getting an answer on my paper. This comes from me struggling to ask the right questions to clarify the problems, and also from a lack of perseverance that I have felt towards some of my classes. I have been able to overcome this lack of perseverance by being able to create an exploration that was fun, with a great partner. This helped bring my attention back to having fun in math while learning the content, instead of just trying to do the work and not care if I retain the work.
Recognizing and Resolving Errors
Through the second semester the only examples I can think of of me and my fellow group mates recognizing and resolving errors is during many exploration seminars. It's not uncommon for 2 or 3 people to have different but similar answers on problems of explorations, and the way that we figure out which is correct is by evaluating the work each student has done. Step by step students take turns walking each other through their approach to the problem and when the realize they had made a mistake, or a mistake is pointed out, the answer to that problem becomes much more clear. This evaluation has helped me to understand where I want wrong in the problem, and why the answer is what is ends up being. Unfortunately, my group and I sometimes try to rush through the seminar to give us time to start on that nights homework, or other class work. We rush through by asking how many people got the same answer, and majority rules, this weakness has affected us by making us want to engage in authentic seminar less, meaning engage in less actual learning.
Reflecting and Synthesizing
A very important part of the exploration process and system is reflecting on what you did in the problems above. This reflecting usually happens in the seminar, so in the last project TJ and I decided to put problems in the middle of the exploration that made the audience reflect on the work they were just doing, and actally understand the process they are going to. A great way that we often reflect in class in by generating a general rule, but because there isn't a general rule, TJ and I asked them to evaluate the process that they had just went through.
For the final project Tj and I had created an exploration that walked people through simple step conversion problems. This exploration exemplified one habit of a mathematician that I did very well but instead of generating multiple ways of approaching a problem, we thought about problems that proved different conversions but that were all still simple. This included having to convert different ways, for example we have a couple of problems using currency, some about weight, and also some about volume. One way we could have expressed this habit more is if we created a problem that helped the audience set up the measurements over each other so they could see how they cross cancel.
Communicating Thinking in a Clear and Accessible Way
Through the second semester I felt like I was much more comfortable conveying my ideas and approach to problems, even if I wasn't sure on the answer. Explorations often throw new content at me and therefor I approach each problem from a problem-solving perspective instead of a math problem. This sometimes leads to me doing problems in a very unconventional way, and when we review the homework the next day, I have had to learn how to walk people through my crazy steps and thinking. Although I am usually able to find some kind of approach to a problem, sometimes I am not able to and need to listen to the ways my peers went. Unfortunately, when I do not understand I often lose sight of actually learning the problem, and instead focus on just getting an answer on my paper. This comes from me struggling to ask the right questions to clarify the problems, and also from a lack of perseverance that I have felt towards some of my classes. I have been able to overcome this lack of perseverance by being able to create an exploration that was fun, with a great partner. This helped bring my attention back to having fun in math while learning the content, instead of just trying to do the work and not care if I retain the work.
Recognizing and Resolving Errors
Through the second semester the only examples I can think of of me and my fellow group mates recognizing and resolving errors is during many exploration seminars. It's not uncommon for 2 or 3 people to have different but similar answers on problems of explorations, and the way that we figure out which is correct is by evaluating the work each student has done. Step by step students take turns walking each other through their approach to the problem and when the realize they had made a mistake, or a mistake is pointed out, the answer to that problem becomes much more clear. This evaluation has helped me to understand where I want wrong in the problem, and why the answer is what is ends up being. Unfortunately, my group and I sometimes try to rush through the seminar to give us time to start on that nights homework, or other class work. We rush through by asking how many people got the same answer, and majority rules, this weakness has affected us by making us want to engage in authentic seminar less, meaning engage in less actual learning.
Reflecting and Synthesizing
A very important part of the exploration process and system is reflecting on what you did in the problems above. This reflecting usually happens in the seminar, so in the last project TJ and I decided to put problems in the middle of the exploration that made the audience reflect on the work they were just doing, and actally understand the process they are going to. A great way that we often reflect in class in by generating a general rule, but because there isn't a general rule, TJ and I asked them to evaluate the process that they had just went through.
Algebra 2 Reflection
Part 1
Representing Exponential Decay Through Half-Lives
Through this semester I learned how to represent exponential decay through the half-life of an element. The project that best represents my understanding of this is POW # 5. This Problem of the week was about 10 lbs of carbon-14 decaying exponentially. Through this project I struggled with just understanding the exponential decay equation, and also finding the function for the amount left after t years. When writing the equation a key realization I made was that the amount of carbon-14 left was being cut in half every, 5370 years. This was the most important part of the problem because that is the most significant information, and without it you don’t know how long it would take for it to day. I read it, but I just wasn’t able to apply that to the problem at first, but once I was able to this POW opened up. During this POW I went to get help from Brandon and he helped explain to me what this problem was asking. I read it but just wasn't sure how to apply that information. After understanding what I was supposed to do I was able to create tables and an equation, receiving a 10/10 on this POW.
Representing Exponential Decay Through Half-Lives
Through this semester I learned how to represent exponential decay through the half-life of an element. The project that best represents my understanding of this is POW # 5. This Problem of the week was about 10 lbs of carbon-14 decaying exponentially. Through this project I struggled with just understanding the exponential decay equation, and also finding the function for the amount left after t years. When writing the equation a key realization I made was that the amount of carbon-14 left was being cut in half every, 5370 years. This was the most important part of the problem because that is the most significant information, and without it you don’t know how long it would take for it to day. I read it, but I just wasn’t able to apply that to the problem at first, but once I was able to this POW opened up. During this POW I went to get help from Brandon and he helped explain to me what this problem was asking. I read it but just wasn't sure how to apply that information. After understanding what I was supposed to do I was able to create tables and an equation, receiving a 10/10 on this POW.
Exploration 12 Problem 2
Habits of a Mathematician
Generating Ideas
Generating ideas is the habit of a mathematician that I have best demonstrated this semester in Algebra 2. The characteristics of a mathematician are being able to formulate a plan while anticipating some major intermediate steps in the problem, also brainstorming multiple approaches to the question. Another important skill that I have shown leading me to think my strongest habit is the ability to show properly and use mathematical tools in the problem.
|
I have proven my ability to generate ideas by clearly representing my approach to most of the POWs, but specifically in POW #6.
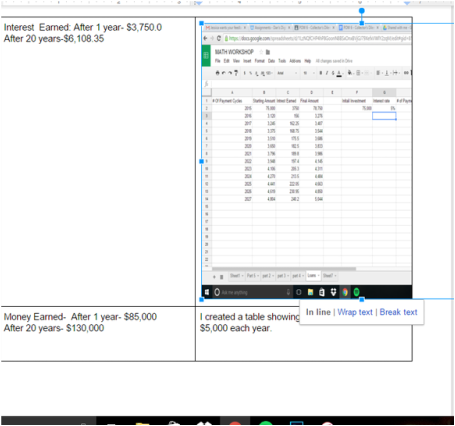
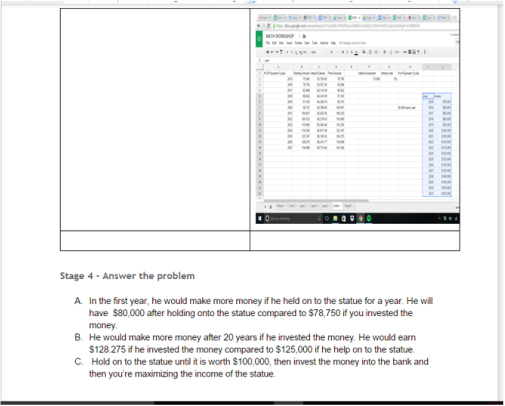
Through this POW I really demonstrated my approach to the problem. I decided to use google spreadsheets to create a function in that could show the amount of money he earned saving the statue, compared to the amount of money he would earn if he invested the money he gained if he were to sell the statue. I showed my approach to the problem by breaking up my steps in this layout that was provided. This POW best shows how I was able to identify and correctly apply the function for growth. In this POW I created 2 tables that each had a different but similar function that showed the money each growing in a different way, and because I was able to use the correct mathematical tool to figure out which situation yielded him the most money. |
The screenshot above is me clearly breaking down my ideas.
|
The screenshots above are on my tables, showing the money earned from each situation.
Spreadsheet Workshop
Below is a link to the spreadsheet worksheet that Izzy and I completed. There are calculators that help calculate speed, time, distance, even interest earned.